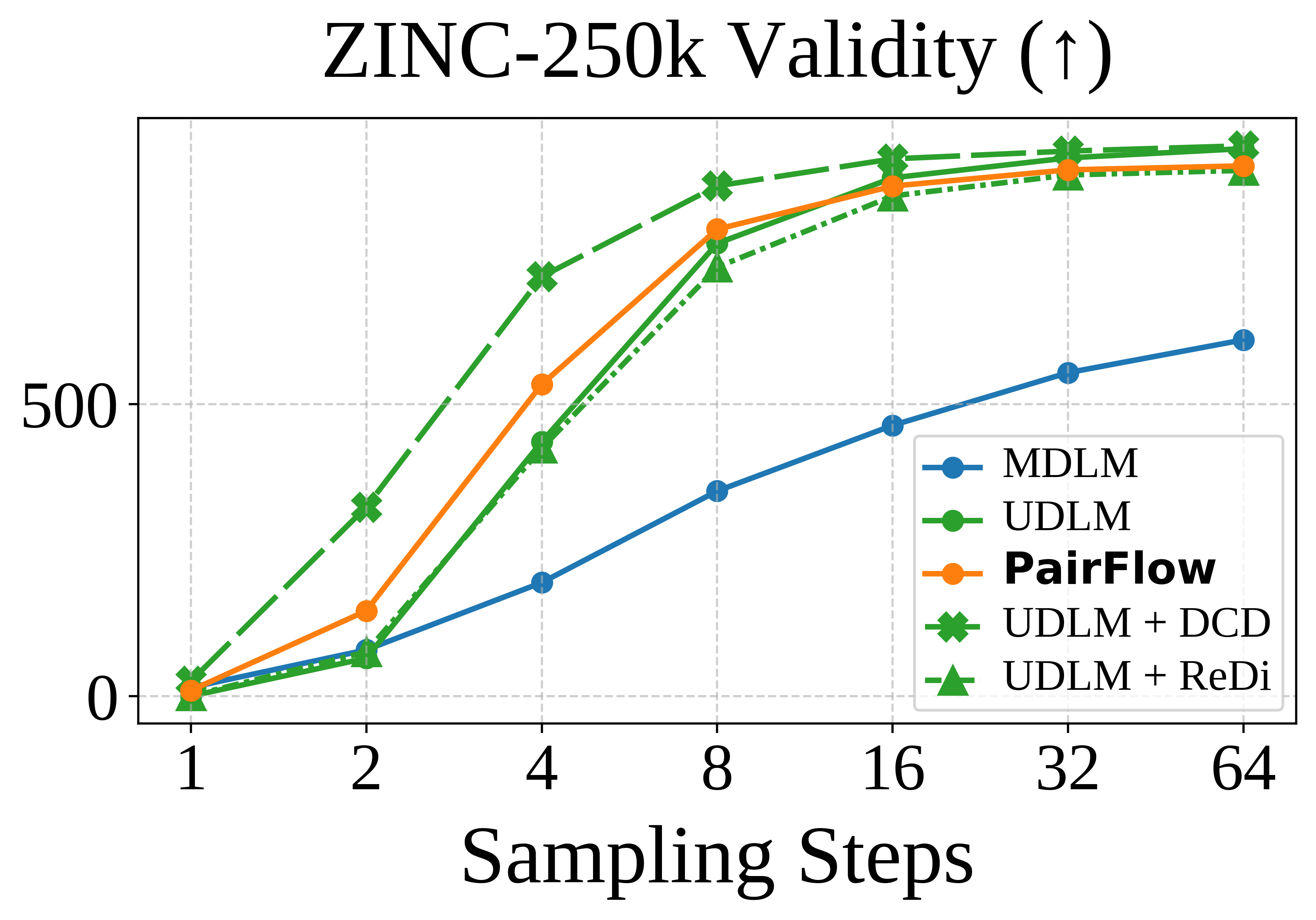
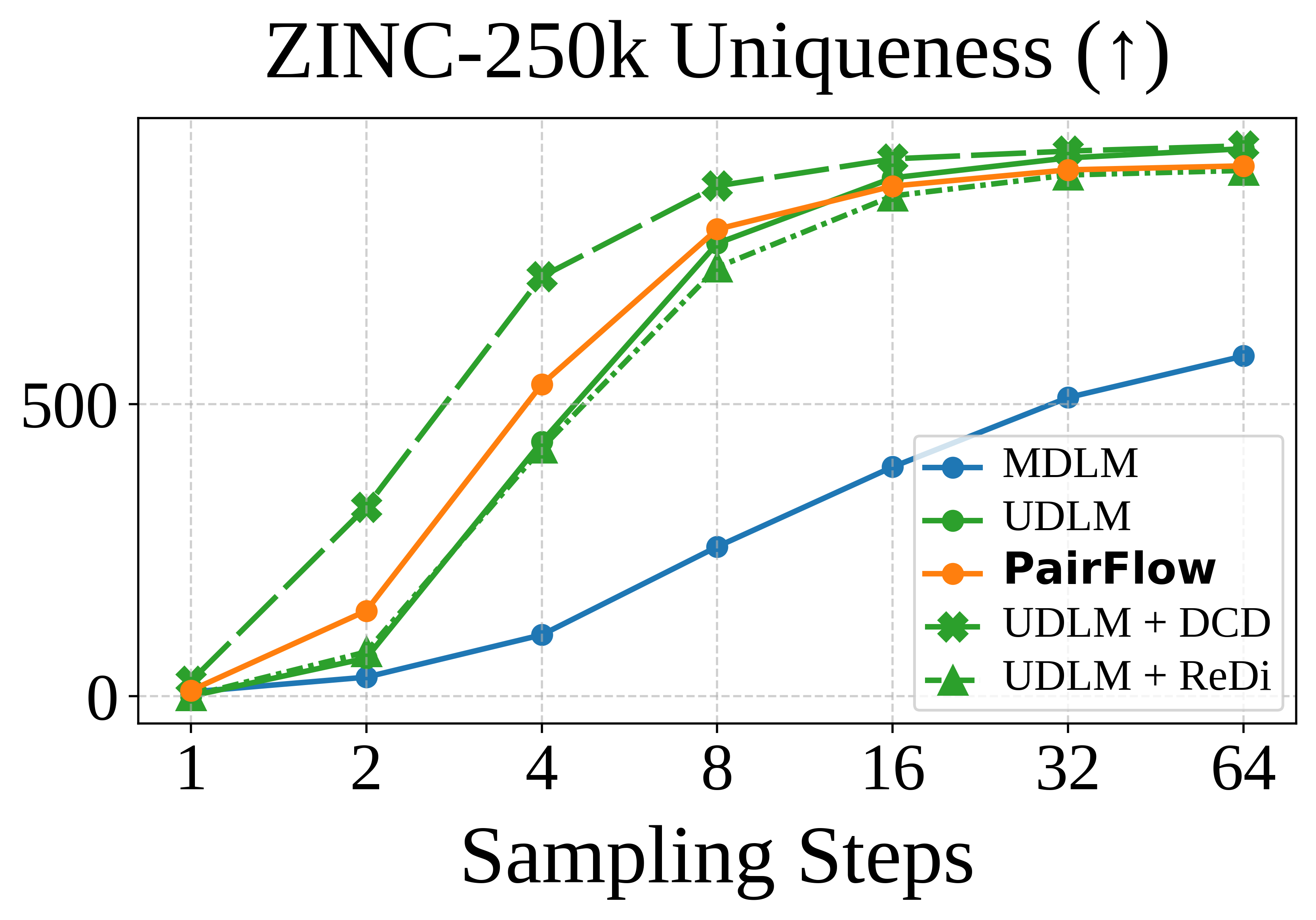
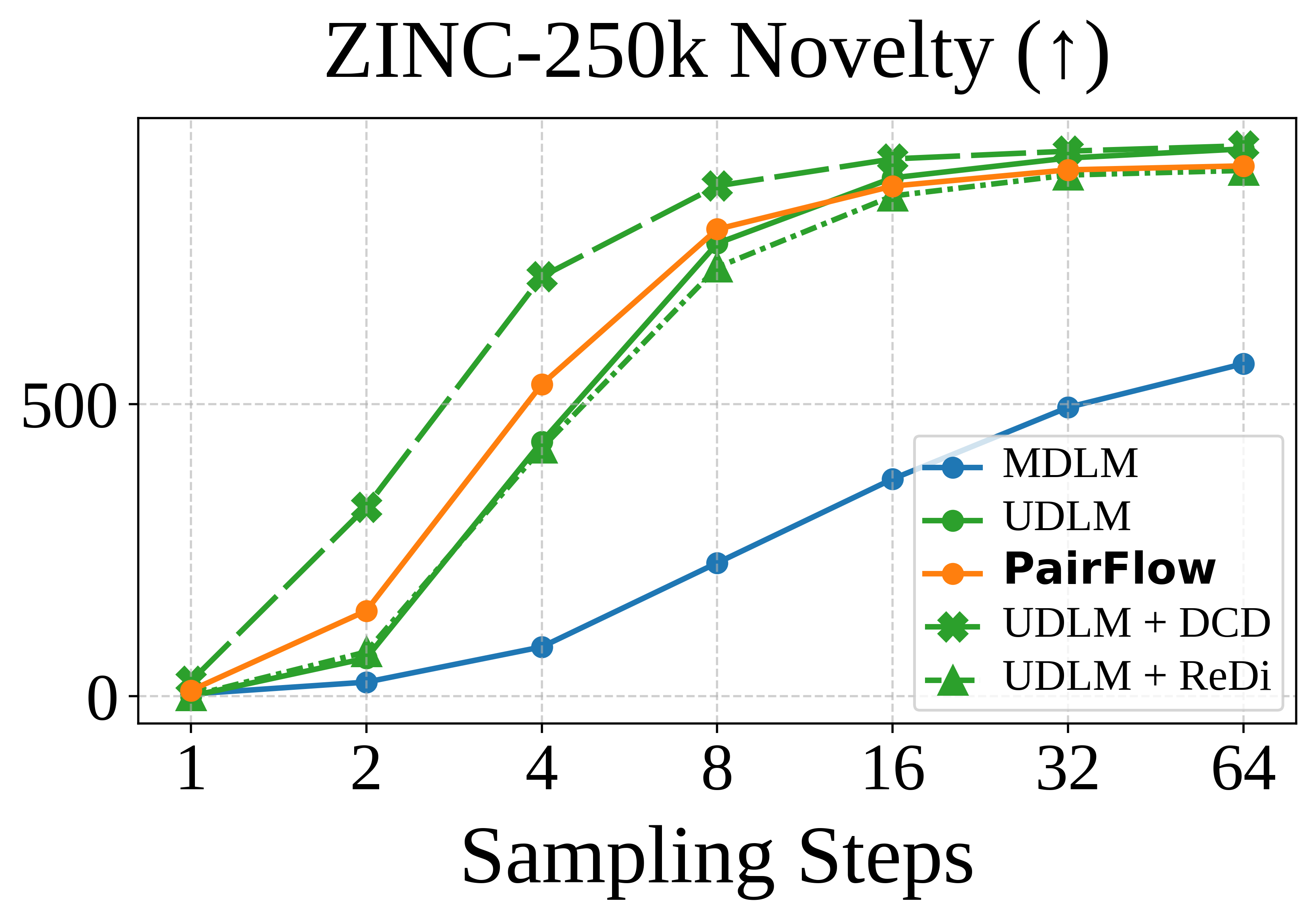
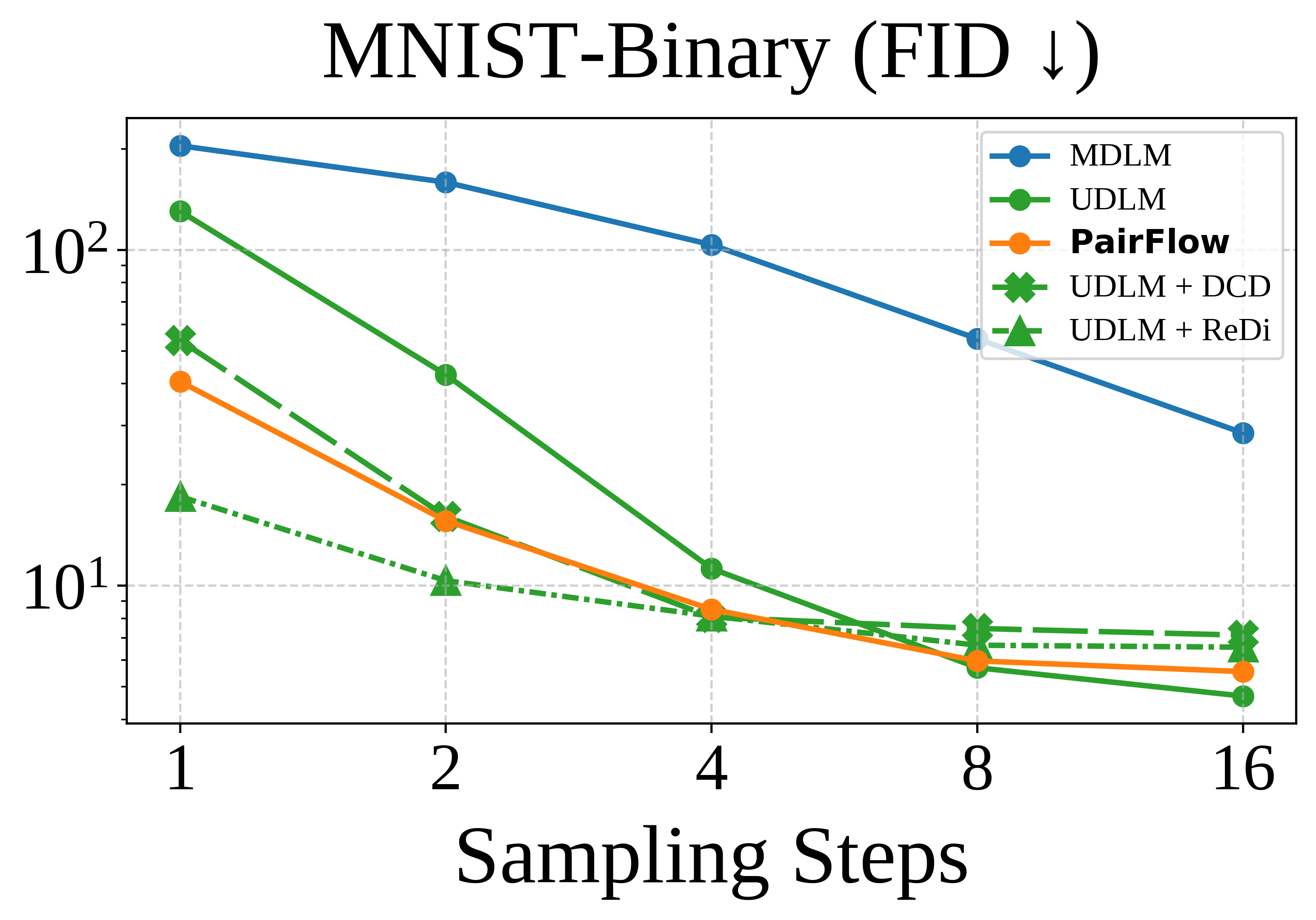
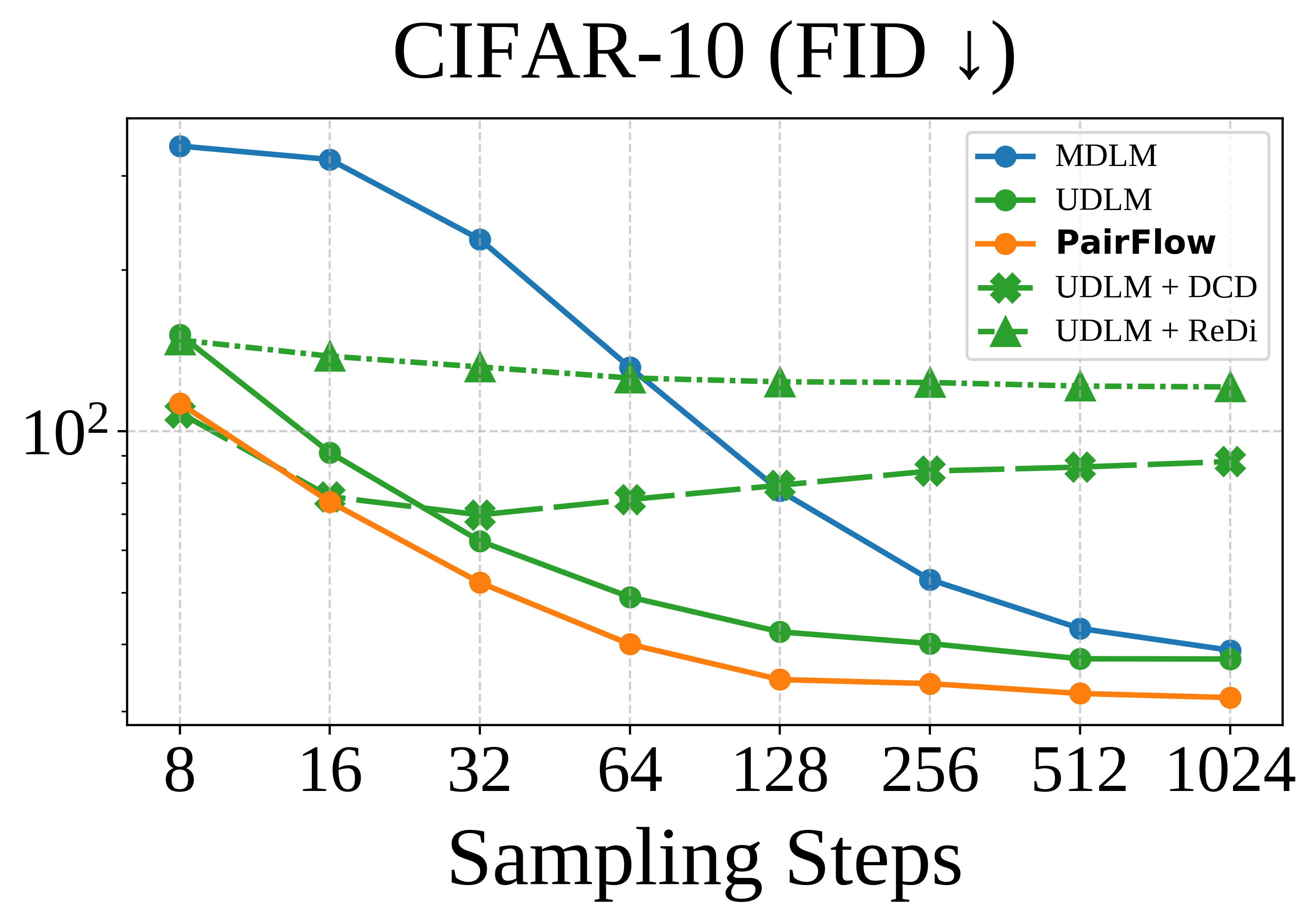
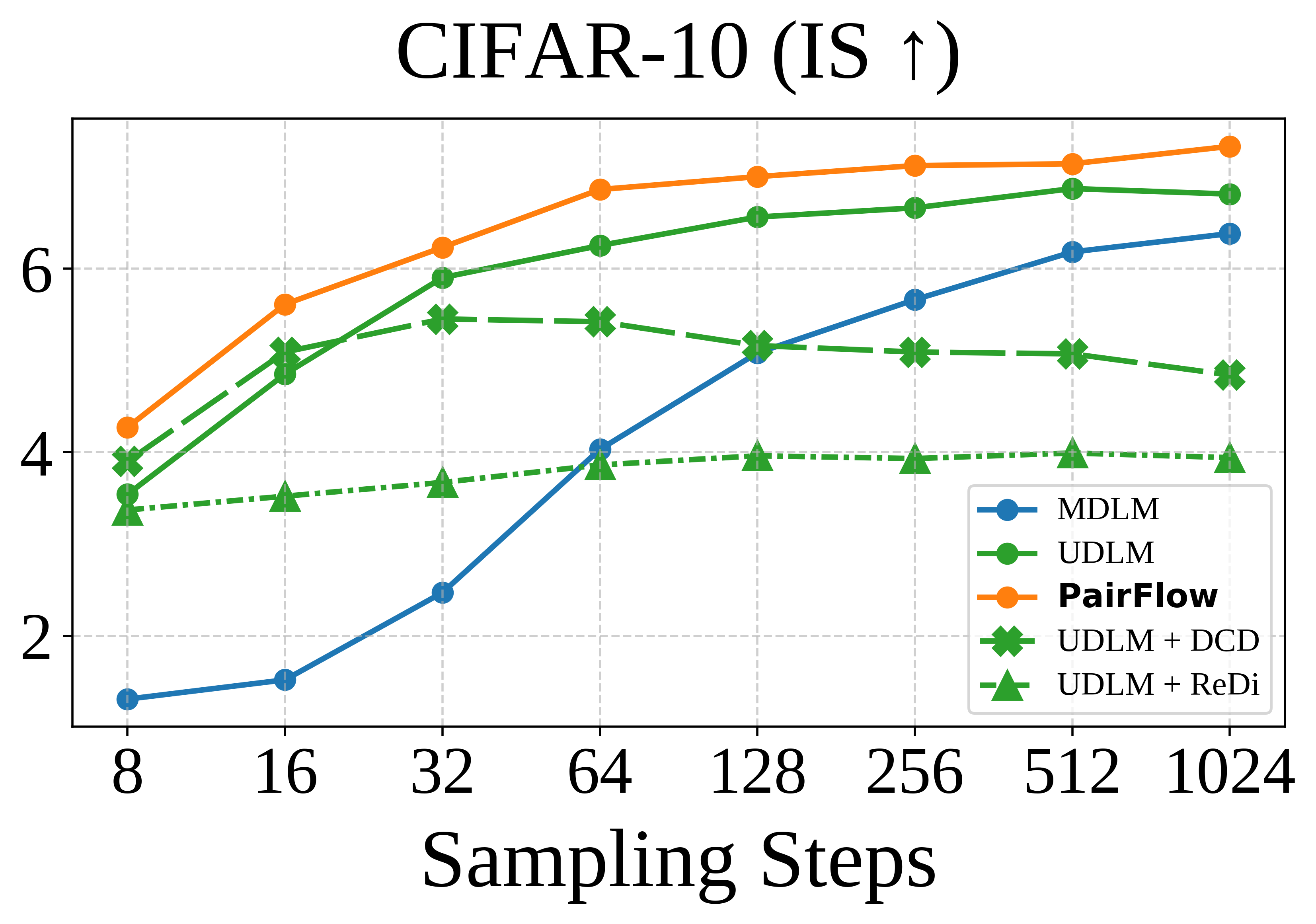
Method
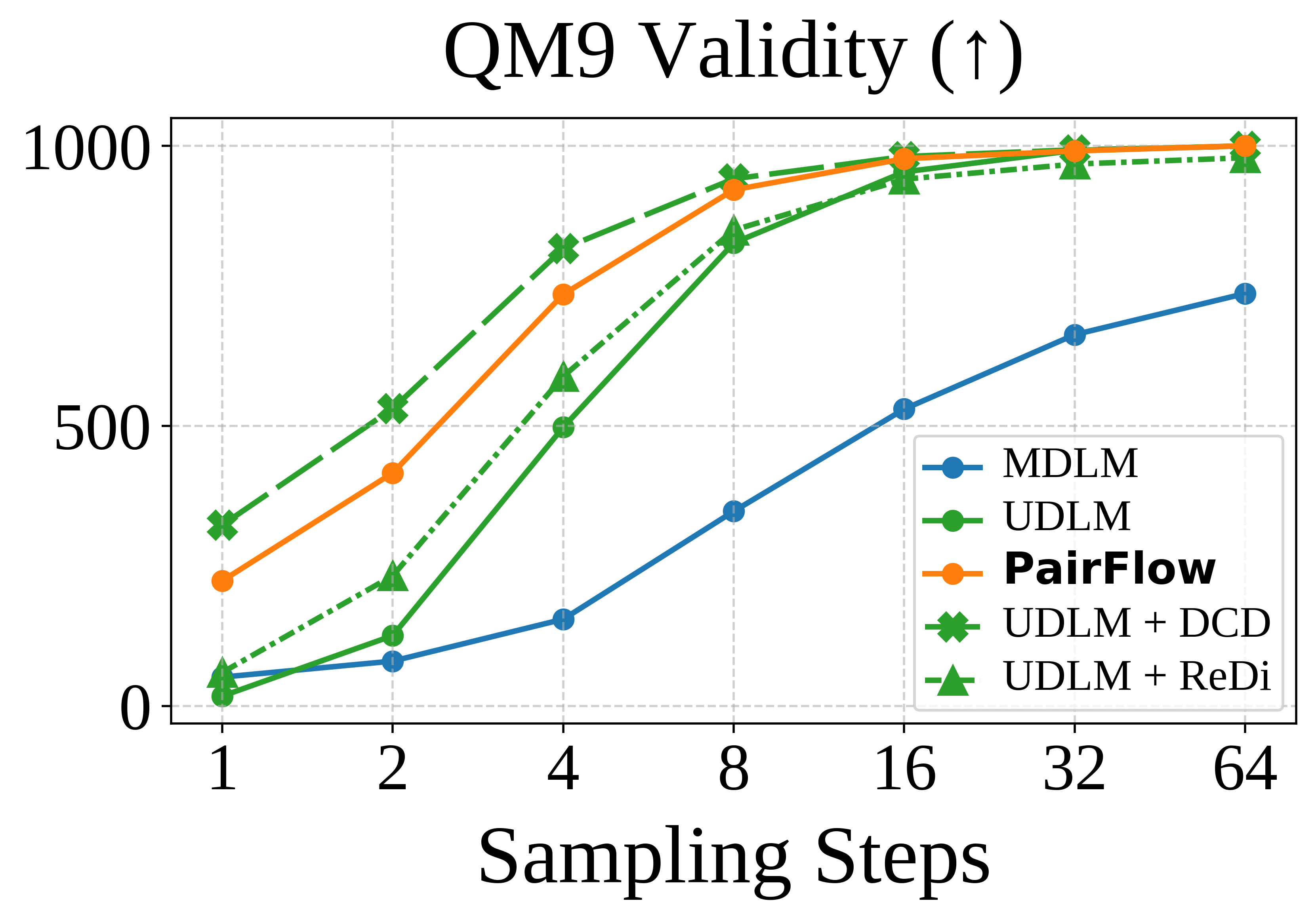
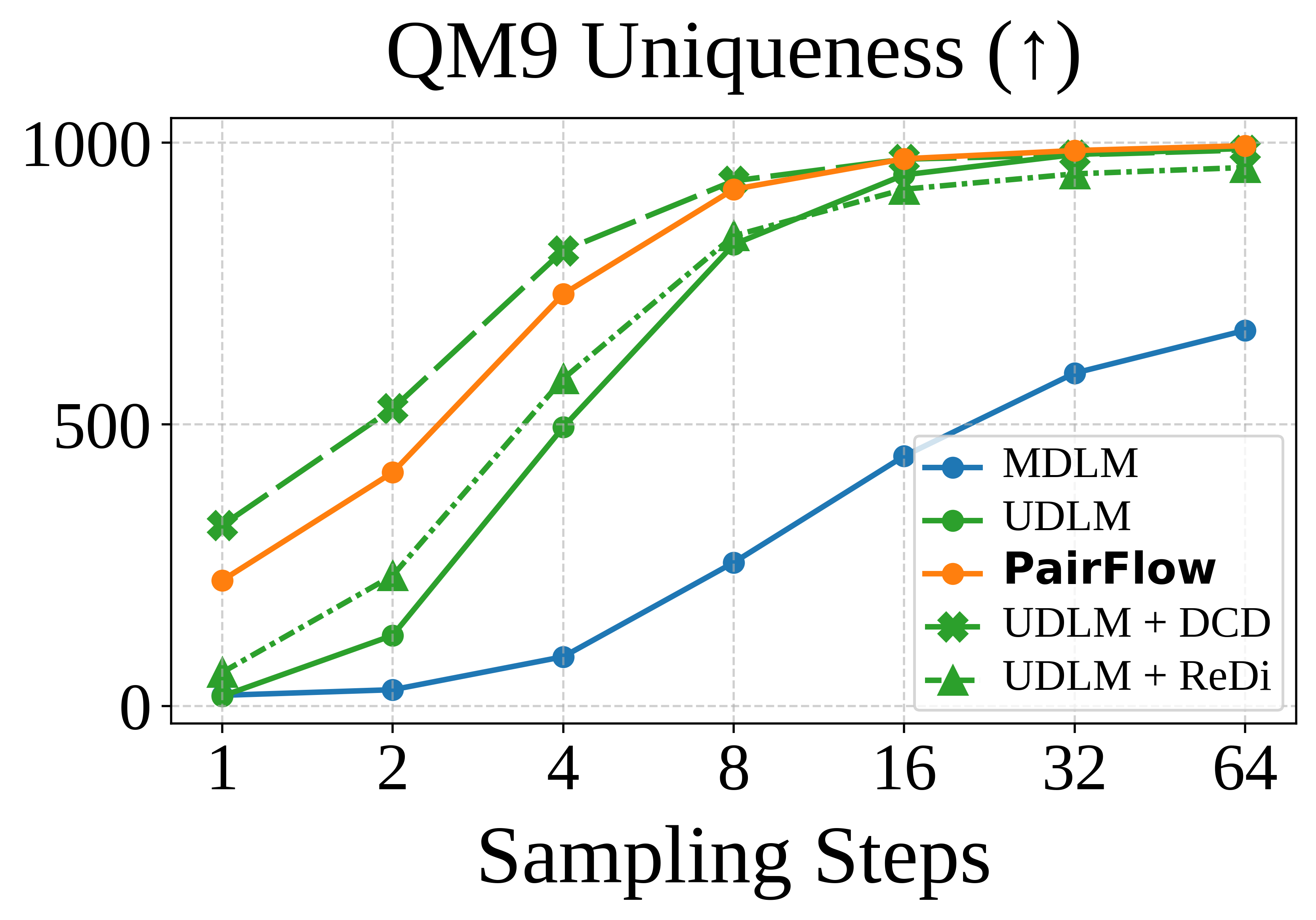
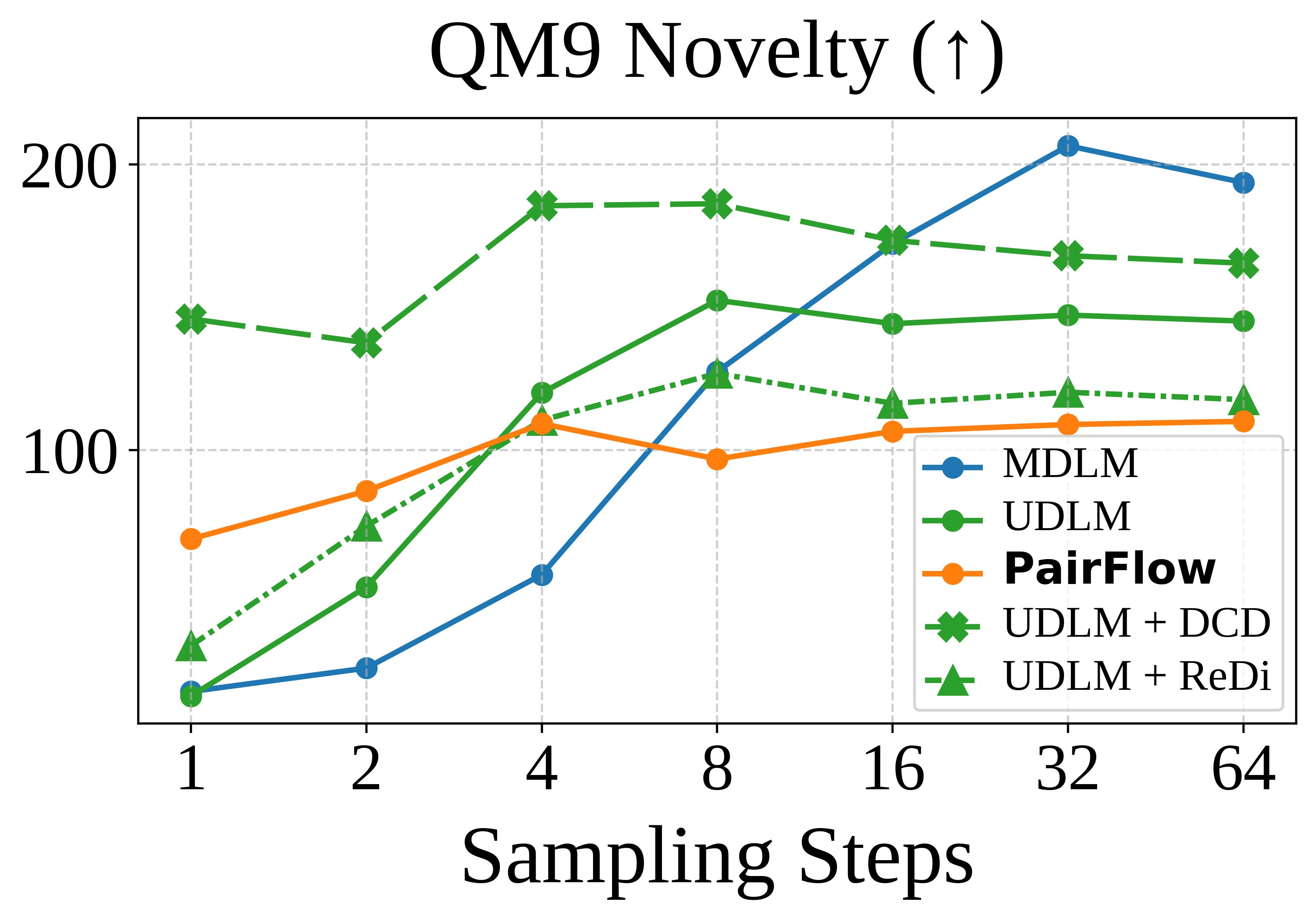
PairFlow is a training framework for DFMs that enables few-step sampling by
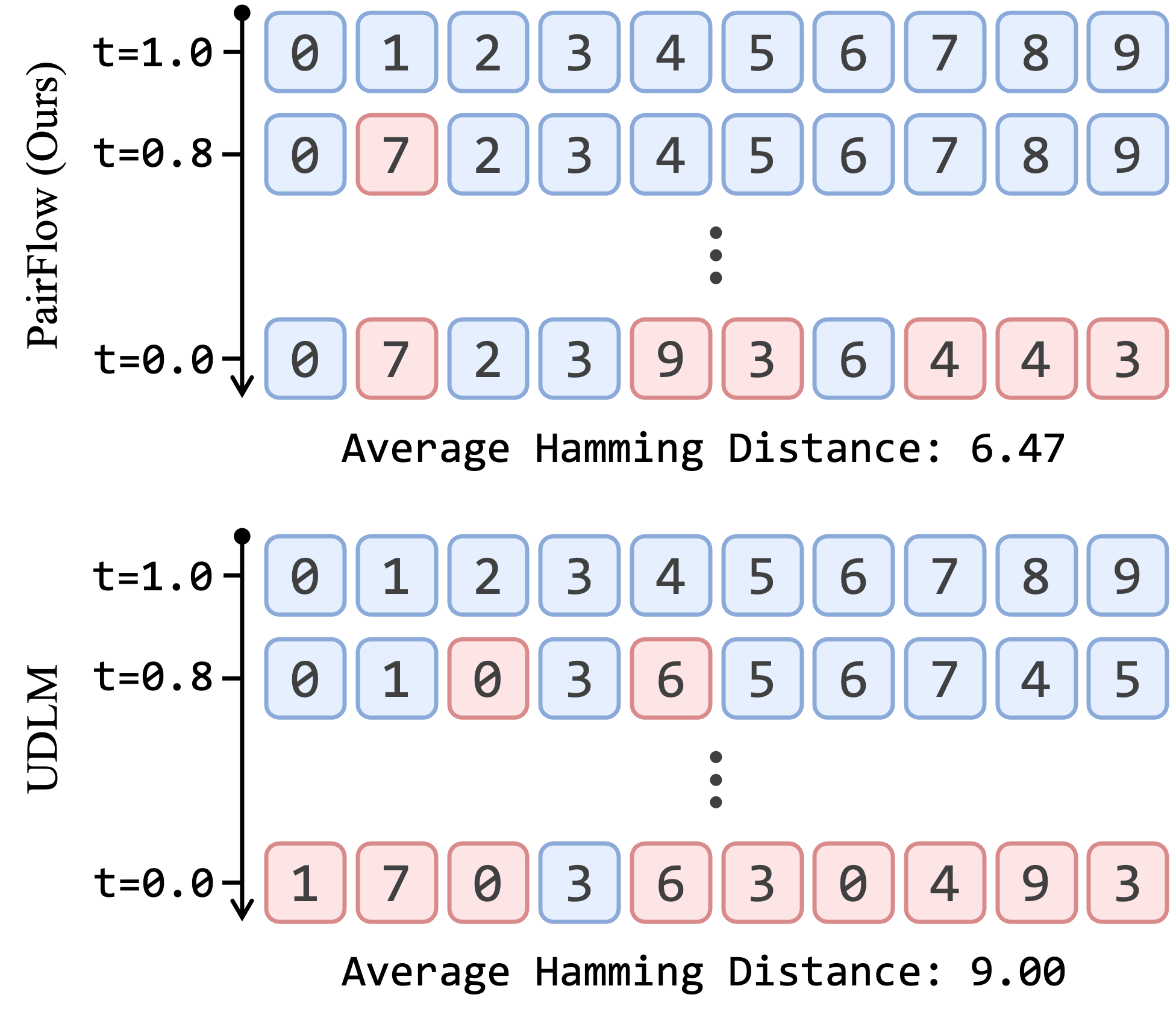
constructing paired
source–target samples using closed-form velocities. While inspired by ReDi-style coupling-driven
training, our approach eliminates the need for a pretrained teacher by using closed-form formulations
and achieves acceleration without finetuning. The algorithm for computing source–target pairs is fully
parallelizable and requires at most 1.7% of compute needed for full model training.

Algorithm 1: Procedure for generating source-target pairs using the
closed-form backward velocity.
Closed-Form Velocity Fields
We derive the closed-form forward velocity field $\hat{v}_t(x^i, z)$ for discrete domains.
For the empirical target distribution $\tilde{q}(x)$, the closed-form denoiser $p_{1|t}(x^i|z)$ and its
associated velocity field $\hat{v}_t(x^i, z)$ are given by:
$$
\begin{align}
p_{1|t}(x^i|z) = \cfrac{\sum_{m=1}^M \delta_{d_{m}^i}(x^i) \gamma^{- h(d_{m}, z)}}{ \sum_{m=1}^M
\gamma^{- h(d_{m}, z)}}, \quad \Longrightarrow \quad
\hat{v}_t(x^i, z) = \frac{\dot\kappa_t}{1 - \kappa_t} \left[p_{1|t}(x^i|z) - \delta_{z}(x^i) \right].
\tag{9}
\end{align}
$$
To effectively identify suitable source-target pairs, we derive the closed-form backward velocity.
Specifically, we first derive the closed-form noise predictor $p_{0|t}(x^i|z)$:
$$
\begin{align}
p_{0|t}(x^i|z) = \delta_{z}(x^i) - \frac{\kappa_t(K \delta_{x^i}(z^i) - 1)}{1 + (K-1)\kappa_t}
\frac{\sum_{m=1}^M \delta_{d_m^i}(z^i)\gamma^{-h(d_m, z)}}{\sum_{m=1}^M \gamma^{-h(d_m, z)}}. \tag{11}
\end{align}
$$
Substituting this into the definition of the backward velocity field, we obtain the desired closed-form
expression:
$$
\begin{align}
\check{v}_t(x^i, z) = \frac{\dot{\kappa}_t(K \delta_{x^i}(z^i)-1)}{1 + (K-1)\kappa_t} \frac{\sum_{m=1}^M
\delta_{d_m^i}(z^i)\gamma^{-h(d_m, z)}}{\sum_{m=1}^M \gamma^{-h(d_m, z)}}. \tag{12}
\end{align}
$$
PairFlow Algorithm
Using the derived closed-form backward velocity, we can efficiently compute source-target pairs. As
outlined in Algorithm 1, starting from a given target data sample $x_1$, we iteratively
apply the backward update rule using $\check{v}_t(x^i, z)$ to trace back the probability path. The final
state $x_0$ reached by this iterative process serves as the source noise. This directly constructs a
well-aligned source-target pair $(x_0, x_1)$ purely from data, effectively eliminating the need for
generating samples from a pretrained teacher model.